随着云计算应用的广泛普及,云计算与互联网的结合也日益紧密,以IPv6为代表的下一代互联网将是未来云计算最优化的选择方案之一。IPv6协议是下一代互联网的核心网络协议,能够更加有效地为云平台及云应用提供网络资源保障和强有力的技术支撑。目前,云用户在享受云计算带来的极大便利的同时,也面临着一些问题,其中重要的问题之一是资源分配问题。为了能够高效地管理资源,实现资源利用率最大化,在云平台资源管理中引入预测技术[1],根据负载情况有效的预测资源使用量,进行合理的资源调度,避免不必要的虚拟机迁移。资源预测技术是优化云计算资源分配的非常有效的方法[2]。
目前资源预测方法较多,对云资源预测的研究大致可以分为两类。第一类预测方法采用经典模型,包括时间序列模型、神经网络模型、支持向量机、马尔科夫模型、贝叶斯模型等。文献[3]利用线性预测方法,如指数移动平均线、二阶自回归移动平均线和移动平均法,预测时间序列数据的工作量。文献[4]为SaaS供应商提供了一个基于自回归移动平均模型(ARIMA)的云工作负载预测模块,提出基于ARIMA模型的预测并使用真实的Web服务器请求数据来评估预测未来工作负载的准确性,此外还评估了预测准确性对资源利用和QoS效率等方面的影响文献[5]利用支持向量机(SVMs)方法的时间序列预测时间序列数据,用于响应时间和吞吐量。文献[6]提出了一种贝叶斯模型,通过在几个数据中心的工作负载模式基础上考虑几个参数,以预测短期和长期的虚拟资源需求。文献[7]分析了云计算的工作负载,并进一步评估了Markov建模和贝叶斯建模等两种预测技术的性能。第二类是针对特定的云工作负载模式进行预测。云环境下现有资源预测模型通常采用单一的预测策略,忽略了其他因素对网络资源的内在作用,导致数据隐含信息丢失量大,所以往往难以取得准确的预测结果的问题。
同时,资源类型的异质性和应用的资源需求变化对云中的工作量预测造成了新的挑战。
针对这一问题,本文提出一种基于ARIMA-Kalman混合模型预测方法。该方法将卡尔曼滤波与自回归积分滑动平均模型相结合,对工作负载所需的资源进行预测。实验结果表明,与单一模型的预测方法相比,该方法具有更高的预测精度,有效的提高了资源利用率,能够很好为虚拟机资源的按需调度提供帮助。
1.预测模型理论
1.1 ARIMA模型
自回归积分滑动平均模型(ARIMA)[8]属于时间序列预测方法,ARIMA模型对采集到的工作负载执行的历史信息进行拟合,由此预测一个负载在未来的执行时间。ARIMA(p , d , q)模型可以表示为:

其中P为自回归阶数,d为差分次数,q为移动平均阶数,为原序列;为白噪声序列,其均值为0;B为后移算子;为自回归算子,为移动算子;为参数,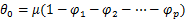 ,为平均数[9]。
,为平均数[9]。
该方法主要分为四个步骤:
第一步,首先确定是否为平稳序列。对于非平稳序列,作差分转换为平稳序列,实现ARIMA模型向ARMA模型的转换。然后,通过序列的自相关系数(AC)和偏自相关系数(PAC)来确定识别AR/MA[9]。
第二步,确定ARIMA模型中的参数。通过穷举参数值对数据进行拟合,评定拟合结果的标准一般是将原序列和拟合的结果序列作差构成残差序列,同时通过比较残差序列的纯随机性来比较拟合程度的好坏[9]。
第三步,将确定的模型对历史数据进行拟合,同时检验拟合的效果。
第四步,使用经过检验的模型,通过对工作负载执行的历史信息进行数据分析,预测未来的负载。
基于ARIMA模型的预测公式如下所示:
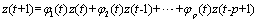
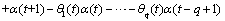 (2)
(2)
其中,z(t+1),z(t),…z(t-p+1)为t+1,t,…,t-p+1时刻对应的工作负载资源利用率的值;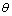 和
和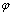 分别代表t时刻的滑动平均项系数和自回归项系数。
分别代表t时刻的滑动平均项系数和自回归项系数。
ARIMA建模优点在于不需要太多的样本序列就可以建立预测模型,但具有低阶ARIMA模型预测精度不高、高阶模型参数不易估计的缺点[10]。
1.2 Kalman滤波模型
卡尔曼滤波(Kalman)是一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法[11]。
Kalman滤波一般步骤如下:
首先要引入一个线性随机微分方程来表示系统状态:
 (3)
(3)
再加上系统的测量值:
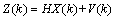 (4)
(4)
其中,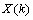 和
和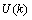 分别表示是
分别表示是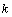 时刻的系统状态和对系统的控制量。
时刻的系统状态和对系统的控制量。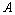 和
和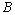 表示系统参数。
表示系统参数。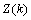 和
和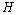 分别表示系统在时刻的测量值和测量系统的参数。
分别表示系统在时刻的测量值和测量系统的参数。 和
和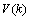 分别表示系统过程和测量的高斯白噪声,其协方差分别是
分别表示系统过程和测量的高斯白噪声,其协方差分别是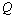 和
和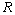 。
。
假设现在的系统状态是K,则可以通过系统的前一状态进行预测得出当前状态,如公式(5)所示:
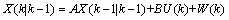 (5)其中,
(5)其中,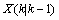 是对当前状态的预测值,
是对当前状态的预测值,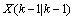 是前一状态最优解,
是前一状态最优解,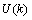 为现在状态的控制量。
为现在状态的控制量。
系统的预测结果已经更新了,则对应的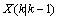 的协方差同时进行更新。我们用
的协方差同时进行更新。我们用 表示
表示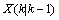 的协方差:
的协方差:
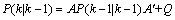 (6)
(6)
式(6)中,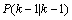 是
是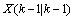 的协方差,
的协方差, 为
为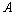 的转置矩阵。公式(5)(6)就是卡尔曼滤波器对系统的预测公式。
的转置矩阵。公式(5)(6)就是卡尔曼滤波器对系统的预测公式。
结合预测值和测量值,可以得到现在状态的最优化估算值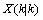 :
:
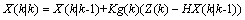 (7)
(7)
其中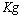 为卡尔曼增益:
为卡尔曼增益:
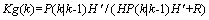 (8)
(8)
通过更新K状态下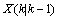 的协方差,实现Kalman滤波持续运行:
的协方差,实现Kalman滤波持续运行:
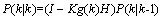 (9)
(9)
其中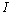 为1的矩阵。当系统进入k+1状态时,
为1的矩阵。当系统进入k+1状态时,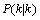 就是公式(6)的
就是公式(6)的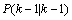 。
。
卡尔曼滤波预测算法有很多优点。它只依赖于递归方法,不需要所有的历史数据。它不仅可以用来处理静止和非平稳的随机过程,还可以用来处理时变和非时变的系统。


